위상정렬은 먼저 비순환 방향 그래프 DAG에서만 사용 가능합니다.
그래프 이론에서 DAG는 노드와 노드간의 방향성을 가진 간선으로 구성된 그래프를 의미합니다.
각 간선이 하나의 노드에서 다른 노드로 방향을 가지며, 일방통행을 합니다.
또한 그래프 내에서 절대 사이클이 없는 것을 의미합니다.
즉, DAG는 방향성이 있고 사이클이 없는 그래프라고 볼 수 있습니다.

위상정렬
위상정렬은 순서가 정해진 작업을 차례대로 수행할때 순서를 결정해주는 알고리즘입니다.
예를 들어서, 라면을 끓이기 위해 물을 먼저 끓어야 합니다. 이때 물을 먼저 끓인다 -> 라면을 끓인다 라는 작업간의 선행 순서가 존재하고 이 선행 순서를 정해주는 알고리즘입니다!
또한 그래프에는 진입차수(In-Degree)와 진출차수(Out-Degree)가 존재합니다.
진입차수는 정점 A로 들어오는 간선의 수를 의미하고, 진출차수는 정점A에서 나가는 간선의 수를 의미합니다.

정점 1로 들어오는 간선은 없으므로 진입차수가 0이고 1에서 출발하는 간선은 2개 있어서 진출차수는 2가 됩니다.
위상정렬을 구현하는 방법은 DFS(진출 차수)를 이용하는 방법과 BFS(진입 차수)를 이용하는 방법 2가지가 존재합니다.
먼저 DFS를 통해 위상정렬을 구현하는 방법은 다음과 같습니다.
다음의 그림과 같은 DAG가 존재합니다.
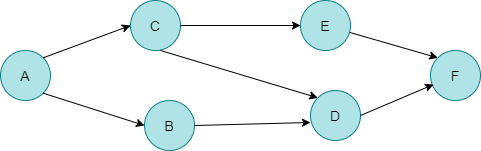
위의 그래프에서 정점간 의존을 파악해보면 다음과 같습니다(선행 작업을 의미합니다..!)
정점 B와 C는 A정점에 의존
정점 D는 C와 B에 의존
정점 E는 C에 의존
정점 F는 정점 D와 E에 의존
위상정렬을 구현하기에 가장 직관적인 방법은, 들어오는 간선이 없는 정점을 찾아서 정렬 결과에 붙이고,
그래프에서 이 정점을 지우는 것을 반복하는 것입니다.
-DFS를 이용해 위상정렬을 구현하는 법-
- 방향성 그래프의 인접 리스트 표현을 준비합니다.
- 방문 기록을 저장할 배열을 생성합니다.
- 빈 스택(stack)을 생성합니다.
- 방향성 그래프의 모든 노드에 대해서 반복합니다.
- 해당 노드를 아직 방문하지 않았다면, DFS 함수를 호출합니다.
- DFS 함수를 정의합니다. 다음과 같은 단계를 수행합니다.
- 현재 노드를 방문으로 표시하고, 현재 노드와 연결된 모든 이웃 노드를 재귀적으로 방문합니다.
- 이웃 노드를 방문하기 전에 DFS 함수를 재귀적으로 호출합니다.
- 현재 노드의 모든 이웃 노드를 방문한 후에 현재 노드를 스택에 삽입합니다.
- 스택을 역순으로 출력하면 위상 정렬된 순서가 됩니다.
왜 이 방법이 성립하는 것일까요?
DFS()의 종료 역순으로 정점을 쭉 늘어놨을떄, 그림과 같이 오른쪽에서 왼쪽으로 가는 간선(u,v)가 있다고 가정해봅시다.
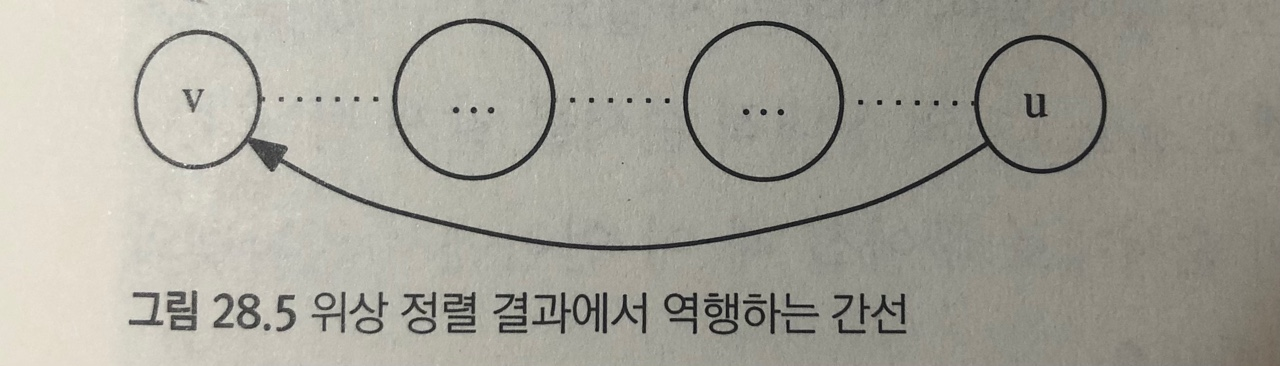
dfs(u)가 종료한 후 dfs(v)가 종료했다
= dfs(u)가 호출되었을 때, dfs(v)는 이미 실행 중이었다
= dfs(v)에서 재귀 호출을 거쳐 dfs(u)가 호출되었다
= 그래프에 v에서 u로 가는 경로가 존재한다
이때 간선 v에서 u로 가는 경로가 존재한다는 말은 사이클이 아닌 그래프 DAG에 모순됩니다.
-> 따라서 dfs의 종료 순서를 역순으로 늘어놓는다면, 그 자체가 위상정렬의 결과가 됩니다.
//참고 - 종만북 코드
//깊이 우선 탐색을 이용한 위상 정렬
vector<int> seen, order;
//깊이 우선 탐색을 진행하며 dfs종료 순서 기록
void dfs(int here){
seen[here] = 1;
for(int there = 0; there < 26; ++there){
if(adj[here][there] && !seen[there])
dfs(there);
}
order.push_back(here);
}
//adj에 주어진 그래프 위상 정렬한 결과 반환
//그래프가 DAG가 아니라면 빈 벡터 반환
vector<int> topologicalSort(){
int n = adj.size();
seen = vector<int>(n, 0);
order.clear();
//dfsAll
for(int i = 0; i<n; ++i){
if(!seen[i]) dfs(i);
}
//dfs 종료 역순으로 뒤집기
reverse(order.begin(), order.end());
//만약 정렬 결과에 역방향 간선이 있다면 DAG가 아니다
for(int i = 0; i<n; ++i){
for(int j = i + 1; j <n; ++j){
if(adj[order[j]][order[i]]) return vector<int>();
}
}
return order;
}
BFS를 이용한 위상 정렬 구현
DFS가 아닌 BFS로도 위상 정렬을 구현할 수 있습니다. 진행 과정은 다음과 같습니다.
- 방향성 그래프의 인접 리스트 표현을 준비합니다.
- 각 노드의 진입차수(In-degree)를 계산합니다.
- 진입차수가 0인 모든 노드를 큐(queue)에 넣습니다.
- 큐에서 노드를 하나씩 꺼내고, 해당 노드와 연결된 모든 이웃 노드의 진입차수를 1씩 감소시킵니다.
- 이웃 노드의 진입차수가 0이 되었다면 큐에 추가합니다.
- 큐가 빌 때까지 4번과 5번 단계를 반복합니다.
- 큐에서 노드를 꺼낸 순서가 위상 정렬된 순서가 됩니다.
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
vector<int> topologicalSort(vector<vector<int>>& graph) {
int numNodes = graph.size();
vector<int> inDegree(numNodes, 0);
vector<int> result;
// 진입차수 계산
for (int i = 0; i < numNodes; i++) {
for (int j = 0; j < graph[i].size(); j++) {
int neighbor = graph[i][j];
inDegree[neighbor]++;
}
}
queue<int> q;
// 진입차수가 0인 노드를 큐에 삽입
for (int i = 0; i < numNodes; i++) {
if (inDegree[i] == 0) {
q.push(i);
}
}
// BFS 수행
while (!q.empty()) {
int node = q.front();
q.pop();
result.push_back(node);
// 해당 노드와 연결된 이웃 노드의 진입차수를 감소시킴
for (int i = 0; i < graph[node].size(); i++) {
int neighbor = graph[node][i];
inDegree[neighbor]--;
if (inDegree[neighbor] == 0) {
q.push(neighbor);
}
}
}
return result;
}
int main() {
vector<vector<int>> graph = {
{}, // 0
{0}, // 1
{0}, // 2
{1, 2}, // 3
{3}, // 4
{2, 4}, // 5
{4, 5} // 6
};
vector<int> result = topologicalSort(graph);
cout << "Topological Sort Order: ";'알고리즘' 카테고리의 다른 글
| 프로그래머스 베스트 앨범 (0) | 2023.06.07 |
|---|---|
| 이분 그래프와 판별법 (2) | 2023.03.15 |
| 프로그래머스 덧칠하기 C++ (0) | 2023.03.03 |
| 프로그래머스 뒤에 있는 큰 수 찾기 C++ (0) | 2023.01.31 |
| 프로그래머스 튜플 C++ (0) | 2023.01.29 |