https://www.acmicpc.net/problem/11497
11497번: 통나무 건너뛰기
남규는 통나무를 세워 놓고 건너뛰기를 좋아한다. 그래서 N개의 통나무를 원형으로 세워 놓고 뛰어놀려고 한다. 남규는 원형으로 인접한 옆 통나무로 건너뛰는데, 이때 각 인접한 통나무의 높이
www.acmicpc.net
문제
남규는 통나무를 세워 놓고 건너뛰기를 좋아한다. 그래서 N개의 통나무를 원형으로 세워 놓고 뛰어놀려고 한다. 남규는 원형으로 인접한 옆 통나무로 건너뛰는데, 이때 각 인접한 통나무의 높이 차가 최소가 되게 하려 한다.
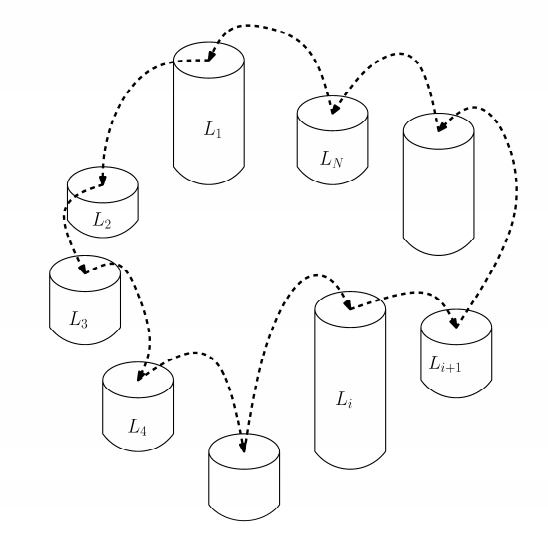
통나무 건너뛰기의 난이도는 인접한 두 통나무 간의 높이의 차의 최댓값으로 결정된다. 높이가 {2, 4, 5, 7, 9}인 통나무들을 세우려 한다고 가정하자. 이를 [2, 9, 7, 4, 5]의 순서로 세웠다면, 가장 첫 통나무와 가장 마지막 통나무 역시 인접해 있다. 즉, 높이가 2인 것과 높이가 5인 것도 서로 인접해 있다. 배열 [2, 9, 7, 4, 5]의 난이도는 |2-9| = 7이다. 우리는 더 나은 배열 [2, 5, 9, 7, 4]를 만들 수 있으며 이 배열의 난이도는 |5-9| = 4이다. 이 배열보다 난이도가 낮은 배열은 만들 수 없으므로 이 배열이 남규가 찾는 답이 된다.
입력
입력은 T개의 테스트 케이스로 이루어져 있다. 첫 줄에 T가 주어진다.
이어지는 각 줄마다 첫 줄에 통나무의 개수를 나타내는 정수 N(5 ≤ N ≤ 10,000), 둘째 줄에 각 통나무의 높이를 나타내는 정수 Li가 주어진다. (1 ≤ Li ≤ 100,000)
출력
각 테스트 케이스마다 한 줄에 주어진 통나무들로 만들 수 있는 최소 난이도를 출력하시오.
통나무가 있고 각 통나무마다 높이가 존재한다.
이 떄, 인접한 통나무로 건너뛰는데, 인접한 통나무의 높이가 최소가 되어야 한다.
예를 들어. 입력으로 5개의 통나무가 들어오고, 각 통나무의 높이가 {2,4,5,7,9}라면,
{2,5,9,7,4}가 된다면 이 배열의 난이도는 4가된다. (인접한 통나무의 높이의 차의 최대값)
일단 이 배열을 어떻게 만들 수 있을 지 생각해보았다.
기존의 {2,4,5,7,9}를 정렬하면 {2,4,5,7,9}이고 기존의 배열이 아닌
새로운 배열이 있다고 생각해보자. (아무것도 들어가지 않은 상태)
--기존 배열--
| 2 | 4 | 5 | 7 | 9 |
--새로운 배열--
이 떄, 새로운 배열도 기존 배열의 크기와 같다.
이제 N개의 기존 배열을 새로운 배열로 옮겨보기 시작한다.
이떄, 2개씩 비교하면서 2개 중 작은 값을 새로운 배열의 처음으로, 2개 중 큰 값을 새로운 배열의 마지막에 넣는다.
{2,4}를 비교해서 작은 2를 처음에, 4를 마지막에 넣는 식이다.
--기존 배열 {2,4} 비교 해서 큰 값을 새 배열의 마지막에, 작은 값을 처음에 넣기 --
| 2 | 4 | 5 | 7 | 9 |
--새로운 배열--
| 2 | 4 |
그리고, 처음과 마지막 값에 대한 갱신이 필요하다.
처음과 마지막에 값을 넣어줬으니깐, 처음위치보다 오른쪽에 값이 들어가고, 마지막 위치보다 왼쪽에 값이 들어간다.
(처음++)/(마지막--) 로 갱신.
그리고 {2,4}의 다음 차례인 {5,7}를 비교해 준다.
처음 ++
마지막 --
--기존 배열 {5,7} 비교 해서 큰 값을 새 배열의 마지막에, 작은 값을 처음에 넣기 --
| 2 | 4 | 5 | 7 | 9 |
--새로운 배열 (5,7중 큰 값을 오른쪽에, 작은 값을 왼쪽에 넣기)--
| 2 | 5 | 7 | 4 |
이제 마지막으로 {9}하나가 남았다.
N의 크기가 홀수 일떄는 새로운 배열의 중앙에 마지막 원소를 넣으면 되고,
N의 크기가 짝수 이면 , 마지막에도 기존의 방식과 마찬가지로 비교해서 넣어주면 된다.
--최종적인 배열 --
| 2 | 5 | 9 | 7 | 4 |
#include <iostream>
#include <algorithm>
using namespace std;
int main(void){
int t;
cin >> t;
while(t--){
int arr[10001]; //기존 배열
int ans[10001]; //새로운 배열
int n;
cin >> n;
for(int i = 0;i<n;i++){
cin >> arr[i];
}
sort(arr,arr+n); //기존 배열 정렬
int l = 0; //처음위치 시작(0)
int r = n-1; //마지막 위치 시작(n-1)
if(n%2 != 0){//N의 크기가 홀수 일 경우
for(int i = 0;i<=n;i=i+2){
/*2개씩 비교하면서 큰 값을 새로운 배열의 오른쪽,
작은 값을 새로운 배열의 왼쪽에 넣고, 왼쪽 오른쪽 갱신 (++, --)
*/
ans[l] = arr[i]; //기존 배열은 오름차순 정렬된 상태이므로 작은 값이 i, 큰 값이 i+1번쨰
ans[r] = arr[i+1];
l++;
r--;
}
ans[n/2] = arr[n-1];//기존 배열의 마지막은 새로운 배열의 중간으로 위치
}
else if(n%2 == 0){ //짝수일경우
/*2개씩 비교하면서 큰 값을 새로운 배열의 오른쪽,
작은 값을 새로운 배열의 왼쪽에 넣고, 왼쪽 오른쪽 갱신 (++, --)
*/
for(int i = 0;i<n;i=i+2){
ans[l] = arr[i];
ans[r] = arr[i+1];
l++;
r--;
}
}
int max = -1; //인접한 통나무의 높이의 차의 최대값 갱신
for(int i = 1;i<n;i++){
if(abs(ans[i] - ans[i-1]) > max){
max = abs(ans[i] - ans[i-1]);
}
}
/*마지막 통나무 - 첫번째 통나무도 고려해야 함 */
if(abs(ans[0] - ans[n-1]) > max){
max = abs(ans[0] - ans[n-1]);
}
cout << max << '\n';
}
}#include <iostream>
#include <algorithm>
using namespace std;
int main(void){
int t;
cin >> t;
while(t--){
int arr[10001]; //기존 배열
int ans[10001]; //새로운 배열
int n;
cin >> n;
for(int i = 0;i<n;i++){
cin >> arr[i];
}
sort(arr,arr+n); //기존 배열 정렬
int l = 0; //처음위치 시작(0)
int r = n-1; //마지막 위치 시작(n-1)
if(n%2 != 0){//N의 크기가 홀수 일 경우
for(int i = 0;i<=n;i=i+2){
/*2개씩 비교하면서 큰 값을 새로운 배열의 오른쪽,
작은 값을 새로운 배열의 왼쪽에 넣고, 왼쪽 오른쪽 갱신 (++, --)
*/
ans[l] = arr[i]; //기존 배열은 오름차순 정렬된 상태이므로 작은 값이 i, 큰 값이 i+1번쨰
ans[r] = arr[i+1];
l++;
r--;
}
ans[n/2] = arr[n-1];//기존 배열의 마지막은 새로운 배열의 중간으로 위치
}
else if(n%2 == 0){ //짝수일경우
/*2개씩 비교하면서 큰 값을 새로운 배열의 오른쪽,
작은 값을 새로운 배열의 왼쪽에 넣고, 왼쪽 오른쪽 갱신 (++, --)
*/
for(int i = 0;i<n;i=i+2){
ans[l] = arr[i];
ans[r] = arr[i+1];
l++;
r--;
}
}
int max = -1; //인접한 통나무의 높이의 차의 최대값 갱신
for(int i = 1;i<n;i++){
if(abs(ans[i] - ans[i-1]) > max){
max = abs(ans[i] - ans[i-1]);
}
}
/*마지막 통나무 - 첫번째 통나무도 고려해야 함 */
if(abs(ans[0] - ans[n-1]) > max){
max = abs(ans[0] - ans[n-1]);
}
cout << max << '\n';
}
}
'알고리즘' 카테고리의 다른 글
| 백준 11536 줄 세우기 C++ (0) | 2022.07.11 |
|---|---|
| 백준 9081 단어 맞추기 C++ (0) | 2022.07.11 |
| 백준 2491 수열 C++ (0) | 2022.07.09 |
| 백준 10971 외판원 순회 2 C++ (0) | 2022.07.06 |
| 너비 우선 탐색 (BFS, Breadth-First Search) (0) | 2022.07.05 |